What Is A Percent Proportion

This section covers:

Percentages and Pct Changes
Ratios and Proportions
Unit Multipliers
Using Percentages with Ratios
More than Practice

Annotation: For more problems with percents and ratios, see the Algebra Word Bug section.

Percentages and Percent Changes

Percentages are something y'all are probably quite familiar with considering of your shopping habits, right? How many times take yous been to the store when everything is 20% off? Do you lot observe how many people around y'all (adults, ordinarily!) have no thought how to figure out what the sale price is? The easiest example of percentages is fifty% off, which means that the item is half price.

Percentages really aren't that difficult if you lot truly sympathize what they are. The give-and-take "percentage" comes from the discussion "per cent", which means "per hundred" in Latin. Remember that "per" usually means "over". So "per cent" literally means "over 100 " or "divided by 100 ". And remember what "of" typically means? I'll write it again, since information technology's so important:

OF = TIMES

When we say " 20% off of something", let'due south translate it to " 20 over (or divided by) 100 — and so times the original price", and that will be the corporeality nosotros decrease from the original price.

Recollect that nosotros cannot use a per centum in math; we demand to plow it into a decimal.To turn a percentage into a decimal, we motion the decimal 2 places to the left (because we demand to divide past 100 ), and if we need to turn a decimal back into a percentage, we motility the decimal 2 places to theright (because we demand to multiply by 100 ).

I like to think of information technology this mode: When we're taking abroad the %, we are afraid of it, so we move 2 decimal places abroad from it (or to the left). When we demand to turn a number into a %, nosotros like information technology, then we motility 2 decimals towards it (or to the right).

Permit'due south become back to our per centum example.If in that location'south a dress we like for say $50 , and it's 20% off ("off" means take-abroad or minus!), we'll do the math to figure out the sales price.This is called a per centum change problem.

Amount of sale: $\displaystyle xx\%\,\,\text{of }\,\$fifty=.ii\times \$fifty=\$10.\,\,\,\,\$50-\$10=\$40$. The dress would be $twoscore .

(See how we had to turn the 20% into a decimal by taking away the % sign and moving ii decimals to the left, or away from it, since nosotros didn't like it?)

We could have too multiplied the original price by $\displaystyle 80\%\,(100\%-20\%)$, or $\displaystyle \frac{{eighty}}{{100}}$, since that's what we'll exist paying if nosotros get 20% off (100% full price minus 20% disbelieve equals 80% discounted price):

Cost of discounted apparel: $\displaystyle fourscore\%\,\,\text{of }\,\$50=.8\times \$50=\$40$. This method has fewer steps.

This shopping example is a per centum decrease problem; the following is the formula for that. Make certain you relate this formula dorsum to the instance above.

$\displaystyle \text{Newer}\,\,\text{lower}\,\,\text{price =}\,\,\text{original}\,\,\text{price}\,\,-\,\,\left( {\text{original}\,\,\text{price}\,\,\times \,\,\left. {\frac{{\text{percentage}\,\,\text{off}}}{{100}}} \right)} \right.$

$\displaystyle \$l-\left( {\$50\,\,\times \,\,\left. {\frac{{twenty}}{{100}}} \right)} \right.\,\,=\,\,\$l-\$x=\$forty$

Observe that we worked the math in the parentheses first (we will become to this in more detail later).

Now let's talk nigh a per centum increase problem, which is also a percent change trouble. A nifty case of a pct increase is the revenue enhancement you pay on this clothes. Tax is a percentage (usually) that y'all add together on to what you pay so nosotros can continue driving on the streets free and going to public school free.

If we demand to add on 8.25% sales tax to the $forty that we are going to spend on the dress, we'll have to know the percent increase formula, but let's first figure it out without the formula. Tax is the amount we take to add that is based on a percent of the price that we're paying for the dress.

The taxation would be 8.25% or .0825 (remember – nosotros don't like the %, so nosotros accept information technology away and move away from it?) times the price of the dress and and then add it back to the price of the dress.

Total price with revenue enhancement: $\displaystyle \$50+(8.25\%\times 50)=\$50+(.0825\times 50)=\$50+\$4.125=\$54.125=\$54.13$.

Note that we rounded upward to two decimal places, since we're dealing with money. Note also that we did the math inside the parentheses beginning.

The full toll of the dress would be $54.13 .

Here's the formula:

$\displaystyle \text{Price}\,\,\text{with}\,\,\text{tax}=\,\,\text{original}\,\,\text{price}+\,\,\left( {\text{original}\,\,\text{toll}\,\,\times \,\,\left. {\frac{{\text{tax}\,\,\text{pct}}}{{100}}} \right)} \correct.$

$\displaystyle \$50+\left( {\$fifty\,\,\times \,\,\left. {\frac{{8.25}}{{100}}} \right)} \right.\,\,=\,\,\$fifty+\left( {\$l\times \left. {.0825} \right)} \right.\,\,=\,\,\$50+\$4.125=\$54.125=\$54.13$

Another mode we can effigy pct increase is to simply multiply the original corporeality by 1 (to make sure we include it) and too multiply it by the revenue enhancement charge per unit and add them together (this is actually using something called distributing, which we'll talk most in Algebra):

$\displaystyle \text{Price}\,\,\text{with}\,\,\text{tax}\,\,\text{=}\,\,\text{original}\,\,\text{price}\,\,\times \,\,\left( {ane+\left. {\frac{{\text{tax}\,\,\text{pct}}}{{100}}} \right)} \correct.$

$\displaystyle \$fifty\,\times \,\left( {1+\left. {\frac{{8.25}}{{100}}} \right)} \correct.=\$fifty\,\times \,\left( {1+\left. {.0825} \right)} \right.=\$50\times one.0825=\$54.125=\$54.13$

If we need to effigy out the actual percent subtract or increment (percent change), nosotros can utilise the following formula:

$\displaystyle \text{Percent Increase}=\frac{{\text{New Toll}-\text{Old Cost}}}{{\text{Quondam Toll}}}\,\times 100$

$\displaystyle \text{Percentage Decrease}\,=\frac{{\text{Old Price}-\text{New Price}}}{{\text{Old Price}}}\,\,\times \,100$

For example, say we want to work backwards to get the percentage of sales taxation that we pay (percent increase). If nosotros know that the original (erstwhile) toll is $50 , and the toll we pay (new price) is $54.thirteen , we could get the % we pay in tax this fashion (note that since we rounded to get the 54.13 , our answer is off a little):

$\displaystyle \text{Percent Increase (Tax)}\,\,=\frac{{54.13-fifty}}{{50}}\,\,\times \,100\,=\,8.26%$

Sometimes we have to work a little backwards in the problem to become the right answer. For case, nosotros may take a problem that says something like this:

Your favorite pair of shoes are on auction for 30% off. The sale toll is $62.30 . What was the original toll?

To practise this problem, we accept to think about the fact that if the shoes are on sale for xxx% , we need to pay 70% for them. Likewise remember that "of = times". We tin can set information technology up this way:

$\displaystyle \,\,.7\,\,\times \,\,?=\$62.30\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,? = \frac{{62.30}}{{.7}} = \$89$

The original price of the shoes would take been $89 before tax.

In the Algebra sections, nosotros will accost solving the post-obit types of per centum issues, just I'll briefly address them here if yous demand to do them at present. If yous don't totally follow how to become the answers, don't worry about it, since we'll cover "discussion issues" later!

What is 20% of 100 ?	$20\%\,\,\text{of}\,\,100=.2\times 100=twenty$
100 is what percentage of 200 ?	$\begin{assortment}{c}100=\,\,?\%\times 200\\\frac{{100}}{{200}}=\,\,?\%\\?=50\cease{array}$
200 is 50% of what number?	$\begin{array}{c}200=50\%\,\,\times \,\,?\\200=.v\,\,\times \,\,?\\200\,\,\text{is half of what}?\\?=400\end{assortment}$

One other way to address percentages is the "$\displaystyle \frac{{\text{is}}}{{\text{of}}}$" fob, which nosotros'll address below.

Ratios and Proportions

Ratios are but a comparison of two numbers. They look a footling scary since they involve fractions, simply they really aren't bad at all. Once again, they are typically used when yous are comparing 2 things — similar toll of ane pair of shoes to some other pair, or possibly even the number of shirts you have compared to the number of jeans yous have.

Let's utilise that as an instance. Let'southward say you have well-nigh 5 shirts for every i pair of jeans you accept, and you figure this same ratiois pretty typical amidst your friends. You can write your ratio in a fraction like $\displaystyle \frac{5}{1}$, or you can use a colon in between the two numbers, like v : 1 (spoken every bit " v to 1 "). The fractions over 1 is actually a rate(this word is related to the word ratio!), for case, just similar when y'all think of miles per hr. Our rate is shirts per one pair of jeans – 5 shirts for every pair of jeans.

Also note that this particular ratio is a unit rate, since the second number (denominator in the fraction) is i .

Let'southward say you know your friend Alicia has 7 pairs of jeans and you're wondering how many shirts she has, based on the ratio or rate of 5 shirts to one pair of jeans. Nosotros can do this with math quite hands by setting up the following proportion, which is an equation (setting two things equal to one another) with a ratio on each side:

$\displaystyle \frac{{\text{shirts}}}{{\text{jeans}}}=\frac{5}{1}=\frac{?}{7}$

How do we figure out how many shirts Alicia has? 1 way is just to think about reducing or expanding fractions. Let's expand the fraction $\displaystyle \frac{5}{1}$ to another fraction that has 7 on the bottom:

$\displaystyle \frac{{\text{shirts}}}{{\text{jeans}}}\,=\,\frac{5}{one}\,=\,\frac{5}{1}\,\times \,1\,=\frac{5}{1}\,\,\times \,\,\frac{seven}{7}\,=\frac{{35}}{7}$

Alicia would accept about 35 shirts.

At present I'm going to also show you a concept called cross-multiplying, which is very, very useful, fifty-fifty when we get into Algebra, Geometry and upwards through Calculus! This is a much easier manner to do these types of problems.

Call up the "butterfly upward" concept when we're comparing fractions, and remember how the fractions are equal when the "butterfly upwards" products are equal?

Nosotros're going to use this concept to set the fractions or ratios equal and then nosotros know how many shirts Alicia has:

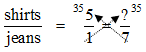
We know that 5 × 7 = 35 , so we demand to know what multiplied past 1 will give us 35 . 35 !! Alicia has 35 shirts!!! See how easy that was?Now if we didn't have the ane as a factor to go to 35, we'd have to divide 35 by the number under the five to get the answer.This is because dividing "undoes" multiplying.

One of my students also suggested to use the "WON" method for proportions. To do this, you set a tabular array with WON at the meridian. "W" stands for Words, "O" stands for Original or Quondam, and "Northward" stands for New (in this instance, for Alicia). Put the words and numbers in the table, and then cross multiply similar we did earlier. Again, we get that Alicia has 35 shirts, based on my proportion of 5 shirts to every pair of jeans, and the fact that she has vii pairs of jeans.

Due west ( W ords)	O ( O ld)	Due north ( North ew)
Shirts	five	?
Jeans	1	7

Let's try a cooking example with proportions, since sometimes the recipe might give yous the amounts in tablespoons, for example, and you lot only take a measuring spoon with teaspoons. We know from the Fractions department that one tablespoon = three teaspoons, and let's say the recipe calls for ii tablespoons. This seems pretty easy to do without the proportion, merely allow'southward set it up anyway, so you tin see how easy it is to use proportions:

$\require{cancel} \displaystyle \frac{{\text{teaspoons}}}{{\text{tablespoons}}}\,\,\,\,\,={}^{6}{{\xcancel{{\frac{3}{1}\,\,\,=\,\,\,\frac{?}{two}}}}^{vi}}$

We know that 3 × 2 = 6 , then nosotros demand to know what multiplied by 1 will give us half dozen . We would need half-dozen teaspoons for our 2 tablespoons.

Now let'south go on to a more complicated instance that relates back to converting numbers dorsum and forth between the metric arrangement and our customary organisation hither.(For more discussion on the metric arrangement, see the Metric System section).

Let's say we have xiii meters of something and we want to know how many feet this is.We can either look upward how many feet are in ane meter, or how many meters are in 1 foot – it really doesn't matter – but nosotros need a conversion number.

Nosotros find that i meter equals approximately 3.28 feet. Let'southward set all this upwardly in a proportion. Think to go along the same unit of measurement either on the tops of the proportion, or on the sides – information technology works both ways:

$\displaystyle \frac{{\text{meters}}}{{\text{meters}}}\,\,=\,\,\frac{{\text{feet}}}{{\text{anxiety}}}\,\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\,\,\frac{{\text{meters}}}{{\text{anxiety}}}\,\,=\,\,\frac{{\text{meters}}}{{\text{feet}}}\,\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\,\,\frac{{\text{feet}}}{{\text{meters}}}\,\,=\,\,\frac{{\text{anxiety}}}{{\text{meters}}}$

Let's solve both two dissimilar means to go the number of feet in xiii meters. Detect that we can turn proportions sideways, motion the " = " sideways as well, and solve – this is sort of how we got from the first equation to the 2nd above.

Proportion	Cantankerous Multiplying	Explanation
$\displaystyle \frac{{\text{meters}}}{{\text{meters}}}\,\,\text{=}\,\,\frac{{\text{feet}}}{{\text{feet}}}$	$\require{cancel} \displaystyle {}^{{42.64}}{{\xcancel{{\frac{1}{{13}}\,\,\,=\,\,\,\frac{{3.28}}{?}}}}^{{42.64}}}$	We know 1 meter is 3.28 anxiety, and then we put these numbers across. We put 13 under the i , since it'due south as well a meter. Then we cross multiply to get $?\,\times 1=42.64$ feet and then there are 42.64 anxiety in 13 meters.
$\displaystyle \frac{{\text{meters}}}{{\text{feet}}}\,\,=\,\,\frac{{\text{meters}}}{{\text{feet}}}$	$\displaystyle {}^{{42.64}}{{\xcancel{{\frac{1}{{3.28}}\,\,\,=\,\,\,\frac{{13}}{?}}}}^{{42.64}}}$	We know 1 meter is 3.28 feet, and so nosotros put those on the left. We put 13 across from the 1 , since it'south also a meter. Then we cantankerous multiply to get $?\,\times one=42.64$ feet so there are 42.64 anxiety in 13 meters.

Hither's an case where we take to do some dividing with our cross multiplying. Try to really empathise why we have to divide by ii to get the answer (it "undoes" the multiplying):

$\displaystyle \frac{5}{two}\,=\,\frac{?}{9}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5\,\,\times \,\,9\,=2\,\times \,?\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,?\,=\,\frac{{5\,\times \,nine}}{ii}\,=\,\frac{{45}}{2}\,=\,\,22\frac{1}{2}$

Unit Multipliers

Nosotros can also use what we call unit of measurement multipliers to change numbers from one unit of measurement to another. The idea is to multiply fractions to get rid of the units we don't want. You probably will use this technique some day when you take Chemistry; it may exist called Dimensional Assay.

Let's say we want to use two unit of measurement multipliers to catechumen 58 inches to yards.

Since we take inches and we want to stop upwards with yards, nosotros'll multiply past ratios (fractions) that relate the units to each other. We tin can practise this because we are really multiplying past " 1 ", since the acme and bottom amounts will be the same (just the units will be unlike). Let's commencement set this up with the units nosotros accept to run across what we'll need to have on the top and the lesser. I put ane 's under the kickoff and concluding items to make them look like fractions:

$\displaystyle \frac{{58\text{ inches}}}{i}\,\,\times \,\,\frac{?}{?}\,\,\times \,\,\frac{?}{?}\,\,=\,\,\frac{{?\text{ yards}}}{i}$

Nosotros need to get rid of the inches unit of measurement on the top and somehow get the yards unit on the top; since the problem calls for ii unit multipliers, we'll include feet to practise this:

$\require{abolish} \displaystyle \frac{{58\text{ }\cancel{{\text{inches}}}}}{1}\,\times \,\frac{{?\text{ }\cancel{{\text{feet}}}}}{{?\text{ }\cancel{{\text{inches}}}}}\,\times \,\frac{{?\text{ }\,\text{yards}}}{{?\text{ }\abolish{{\text{feet}}}}}\,=\,\frac{{\text{? }\,\text{yards}}}{\text{1}}$

Now but fill in how many inches are in a pes, and how many anxiety are in a yard, and we can become the reply with real numbers:

$\displaystyle \frac{{58\text{ }\cancel{{\text{inches}}}}}{1}\,\times \,\frac{{1\text{ }\cancel{{\text{foot}}}}}{{12\text{ }\cancel{{\text{inches}}}}}\,\times \,\frac{{1\text{ chiliad}}}{{3\text{ }\cancel{{\text{feet}}}}}\,=\,\frac{{58\times i\times 1\text{ yards}}}{{1\times 12\times 3}}\,=\,\frac{{58}}{{36}}\text{ }\,\text{yards}\,=\,\frac{{29}}{{18}}\text{ }\,\text{yards}$

Here'southward another example where nosotros employ ii unit of measurement multipliers since we are dealing with square units:

Use two unit multipliers to catechumen 100 square kilometers to square meters.

$\displaystyle \frac{{100\text{ }\cancel{{\text{kilometers}}}\times \cancel{{\text{kilometers}}}}}{1}\,\times \,\frac{{1000\text{ meters}}}{{one\text{ }\cancel{{\text{kilometer}}}}}\,\times \,\frac{{1000\text{ meters}}}{{ane\text{ }\cancel{{\text{kilometer}}}}}\,=\,100,000,000\,\, \text{meter}{{\text{due south}}^{2}}$

Using Percentages with Ratios

Now let'due south revisit percentages and show how proportions can help with them besides! One play a trick on to use is the $\displaystyle \frac{{\text{is}}}{{\text{of}}}$ and $\displaystyle \frac{{\text{part}}}{{\text{whole}}}$ tricks. You can remember these since the give-and-take that comes first in the alphabet ("is" and "part") are on the top of the fractions.

You can typically solve pct problems by using the post-obit formula:

$\displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{\text{ }\!\!\%\!\!\text{ }}{{100}}$

What this means is that the number around the "is" in an equation is on top of the proportion, and the number that comes afterward the "of" in an equation is on bottom of the proportion, and the percentage is over the 100 .

You can also think of this as the post-obit, but y'all take to recollect that sometimes the part may be actually exist bigger than the whole (if the percent is greater than 100):

$\displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\text{ }\!\!\%\!\!\text{ }}{{100}}$

Here are some examples, using the aforementioned problems that we did in a higher place in the Percentages department. (Later, in the Algebra section, we'll learn how to interpret math word issues similar these word-for-word from English to math.)

What is 20% of 100 ?Since we know that the 20 of the % part, we put that over the 100. The 100 comes afterward the "of", so we put that on the bottom. Also, we're looking for the "part" of the "whole" here.

$\displaystyle \frac{{\text{is}}}{{\text{of}}}=\,\frac{\%}{{100}}\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{?}{{100}}=\frac{{20}}{{100}}\,\,\,\,\,\,\,\,\,?=20$

100 is what percent of 200 ? The 100 is close to the "is" then we put that on the top. The 200 comes after the "of", so nosotros put that on the bottom. Also, we know the 100 is the "part" of the 200 .

$\displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{\%}{{100}}\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\frac{{\text{role}}}{{\text{whole}}}=\frac{\%}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{100}}{{200}}=\frac{{?\,\,\,\%}}{{100}}\,\,\,\,\,\,\,\,\,?=fifty$

200 is 50% of what number? The 200 is shut to the "is" and we don't know what the "of" is. The l is the percentage. Likewise, 200 is the "part", so we need to discover the "whole".

$\displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{%}{{100}}\,\,\,\,\,\,\,\text{or}\,\,\,\,\,\frac{{\text{part}}}{{\text{whole}}}=\frac{%}{{100}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{200}}{?}=\frac{{50}}{{100}}\,\,\,\,\,\,\,\,\,?=400$

Hither are a few more than issues on rates and percentages:

Percentage Problem	Solution
1 serving of cashews contains ix grams of carbs, which is five% of a recommended daily allowance. What is the total recommended daily assart of carbs?	Use the equation $\displaystyle \frac{{\text{role}}}{{\text{whole}}}=\frac{\%}{{100}}$, where the role is 9 grams, and the percent is 5 : $\displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}:\,\,\,\,\frac{\text{nine}}{x}=\frac{5}{{100}};\,\,\,\,5x=900;\,\,\,x=180\,\text{grams}$
Two tablespoons of peanut butter contain 190 calories. What percent of a 2200 -calorie diet is contained in 2 tablespoons of peanut butter?	Use the equation $\displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}$, where the role is 190 calories, and the whole is 2200 calories: $\displaystyle \frac{{\text{function}}}{{\text{whole}}}=\frac{\%}{{100}}:\,\,\,\,\frac{{\text{190}}}{{2200}}=\frac{p}{{100}};\,\,\,\,2200p=19000;\,\,\,p=eight.64\%$
A fridge is normally $1200 , but is discounted to $790 . What percent of the original price is paid? What is the percentage discount?	Apply the equation $\displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}$ or $\displaystyle \frac{{\text{is}}}{{\text{of}}}=\frac{\%}{{100}}$, where the part (or "is") is $790 , and the whole (or "of") is $1200 : $\displaystyle \frac{{\text{function}}}{{\text{whole}}}=\frac{\%}{{100}}:\,\,\,\,\frac{{\text{790}}}{{1200}}=\frac{p}{{100}};\,\,\,\,1200p=79000;\,\,\,p=65.83\%$ This is the percent of the original price paid. The percent of the disbelieve is $100\%-65.83\%=34.17\%$. To get the percent discount, nosotros could have too used the formula: $\displaystyle \text{Per centum Subtract}=\frac{{\text{Old Price}-\text{New Price}}}{{\text{Quondam Price}}}\,\times \,100=\frac{{\text{1200}-\text{790}}}{{\text{1200}}}\,\times 100=34.17\%$
A product costs $44 to purchase from a manufacturer, and information technology sells for $lxx . What is the percent increase on this production, to the nearest whole percent?	Use the equation $\displaystyle \text{Percent Increase}\,=\frac{{\text{New Price }-\text{ Erstwhile Price}}}{{\text{Old Price}}}\,\times \,100$, where the old toll (cost) is $44 and the new (sales) cost is $70 : $\displaystyle \frac{{\text{New Price}-\text{Old Toll}}}{{\text{Old Toll}}}\,\times \,100=\frac{{\text{70}-\text{44}}}{{\text{70}}}\,\times \,100=37.xiv\%$
The recommended daily assart for sugar is about 24 grams. One serving of a certain cookie has xv grams of sugar. What is the per centum of the daily recommended allowance of saccharide in 1 serving of this cookie?	Use the equation $\displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}$, where the part is 15 grams, and the whole is 24 grams: $\displaystyle \frac{{\text{part}}}{{\text{whole}}}=\frac{\%}{{100}}:\,\,\,\,\frac{{\text{15}}}{{24}}=\frac{p}{{100}};\,\,\,\,24p=1500;\,\,\,p=62.v\,\text{ }\!\!\%\!\!\text{ }$

Remember also – if you're not quite sure what you're doing, call back of the problems with easier numbers and see how yous're doing it! This tin help a lot of the time.

Larn these rules and practise, practice, do!

Click on Submit (the arrow to the right of the problem) to solve this problem. Y'all tin can too type in more problems, or click on the 3 dots in the upper right hand corner to drill downward for case problems.

If y'all click on "Tap to view steps", you will go to theMathway site, where y'all tin register for thetotal version (steps included) of the software. You lot can even become math worksheets.

You lot can also go to theMathway site here, where you tin annals, or but utilise the software for free without the detailed solutions. There is fifty-fifty a Mathway App for your mobile device. Savour!

On to Negative Numbers and Absolute Value– you are gear up!!